[자료구조] 8.트리

8장 트리

8장. 학습 목표

트리의 개념과 용어들을 이해한다

이진 트리의 표현 방법을 2가지 이해한다.

이진트리의 순회방법들과 연산들을 이해한다.

힙의 동작 원리와 효율성을 이해한다.

배열 구조를 이용한 힙의 구현 방법을 이해한다.

이진트리와 힙을 문제 해결에 활용할 수 있다.

8.1 트리란?

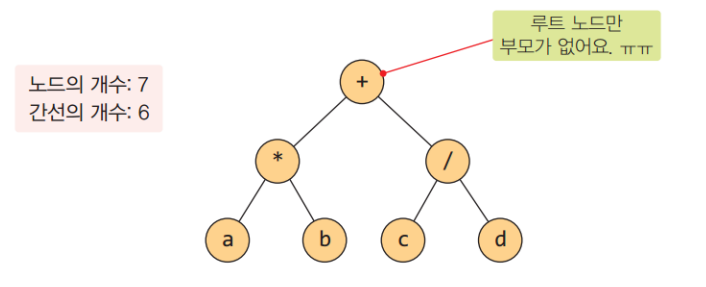
트리는 계층적인 구조를 가지며, 노드(Node)와 간선(Edge)으로 구성된 비선형 자료구조입니다. 노드는 데이터를 저장하고 간선은 노드들을 연결합니다. 트리는 하나의 **루트(Root) 노드**에서 시작하여 다양한 자식(Child) 노드들로 분기되는 구조를 가지며, 각 자식 노드는 부모(Parent) 노드에 의해 생성됩니다.

트리에서 사용되는 용어들은 다음과 같습니다:

루트(Root): 트리의 가장 상위에 있는 노드로, 다른 모든 노드들은 루트 노드의 자식이거나 자손입니다.
부모(Parent): 어떤 노드의 바로 위에 있는 노드를 부모 노드라고 합니다.
자식(Child): 어떤 노드의 바로 아래에 있는 노드를 자식 노드라고 합니다.
형제(Sibling): 같은 부모를 가지고 있는 노드들을 형제 노드라고 합니다.
조상(Ancestor): 어떤 노드의 위에 있는 모든 노드들을 그 노드의 조상 노드라고 합니다.
자손(Descendant): 어떤 노드 아래에 있는 모든 노드들을 그 노드의 자손 노드라고 합니다.
차수(Degree): 어떤 노드의 자식 노드의 수를 차수라고 합니다.
잎 노드(Leaf Node): 자식이 없는 노드를 잎 노드 또는 단말 노드라고 합니다.
서브트리(Subtree): 트리 내에서 특정 노드와 그 자손 노드들로 구성된 부분 트리를 서브트리라고 합니다.

트리는 계층적인 관계를 표현하기에 용이하며, 다양한 응용 분야에서 사용됩니다. 예를 들어, 파일 시스템의 디렉토리 구조, 조직도, 계층적인 데이터 구조 등에서 트리 구조가 적용될 수 있습니다.

8.2 이진 트리

이진 트리는 순환적으로 정의된다.

이진트리의 종류와 성질

이진트리의 표현 방법

이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식을 가질 수 있는 트리입니다. 이진 트리는 부모 노드와 최대 두 개의 자식 노드로 구성되며, 왼쪽 자식과 오른쪽 자식 노드를 구분합니다. 각 노드는 하나의 데이터를 저장하며, 자식 노드가 없을 경우 잎 노드(리프 노드)가 됩니다.

이진 트리는 여러 가지 표현 방법이 있습니다. 그 중에서도 가장 일반적인 방법은 포화 이진 트리와 완전 이진 트리입니다.

포화 이진 트리(Full Binary Tree):
- 모든 레벨에서 노드들이 꽉 찬 상태인 이진 트리입니다.
- 즉, 모든 내부 노드가 두 개의 자식을 가지고 있고, 잎 노드를 제외한 모든 노드의 차수가 2인 트리입니다.
- 레벨당 최대 노드 수는 2^k개로, 전체 노드 수는 2^(k+1) - 1개입니다.
완전 이진 트리(Complete Binary Tree):
- 레벨이 k인 완전 이진 트리는 레벨 k-1까지는 포화 이진 트리이고, 마지막 레벨은 왼쪽부터 오른쪽으로 노드들이 순서대로 채워진 트리입니다.
- 모든 레벨에서 노드들은 왼쪽부터 채워지며, 마지막 레벨에서 오른쪽에 빈 자리가 있을 수 있습니다.
- 레벨별로 왼쪽에서 오른쪽으로 순서대로 노드가 추가되기 때문에 배열이나 리스트로 효율적으로 표현될 수 있습니다.

포화 이진 트리와 완전 이진 트리는 트리의 형태와 노드의 배치에 따라 다르게 구성됩니다. 이러한 특징을 이용하여 트리를 저장하고 효율적으로 탐색하거나 연산을 수행할 수 있습니다.

이진 트리의 성질

노드의 개수가 n개이면 간선의 개수는 n-1

높이가 h 이면 h ~ 2^h - 1 개의 노드를 가짐

n개의 노드를 가지는 이진 트리 높이: [log2(n+1)] ~ n

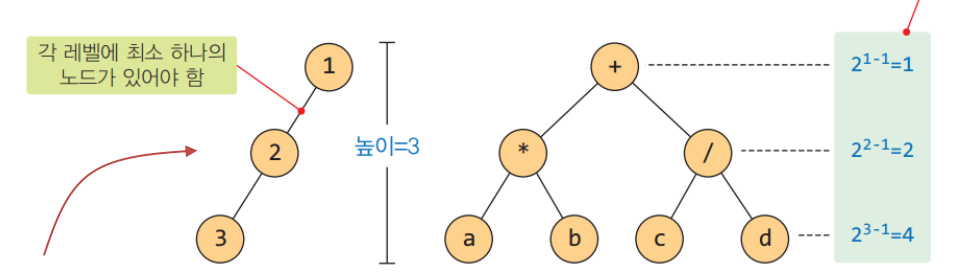
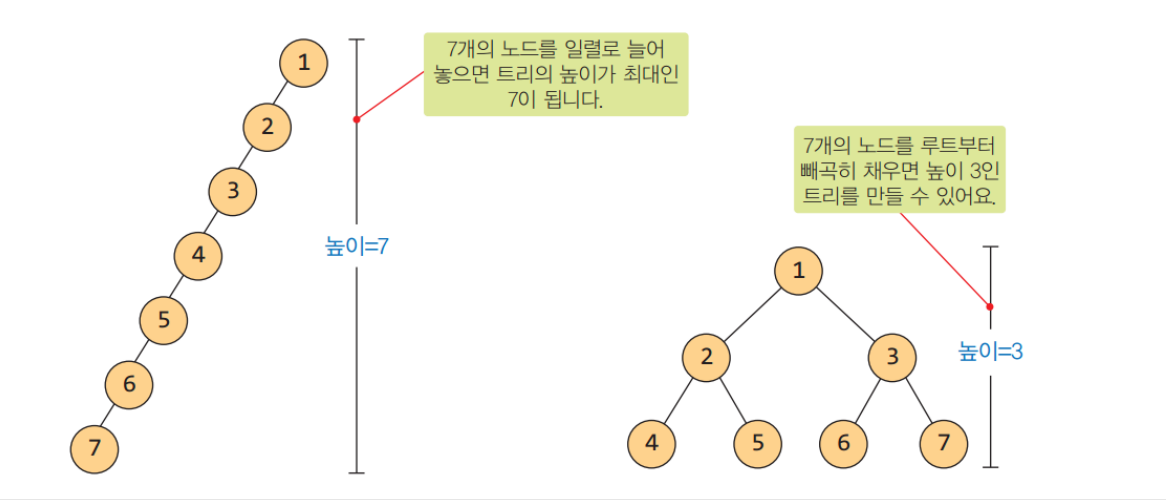
n개의 노드를 가지는 높이 h의 이진 트리가 가질 수 있는 노드 개수의 최댓값: 2^h-1, n <= 2^h - 1, h >= log2(n+1), h는 정수

이진 트리를 표현하는 방법은 주로 배열 표현법(Array Representation)과 링크 표현법(Link Representation) 두 가지가 있습니다.

배열 표현법 (Array Representation):
- 이진 트리의 노드를 배열에 저장하는 방법입니다.
- 배열을 사용하여 트리의 각 노드를 인덱스로 표현합니다.
- 일반적으로 완전 이진 트리의 경우에 사용됩니다.
- 각 노드의 자식 노드는 배열에서 특정한 위치에 저장됩니다.
- 부모와 자식 간의 관계를 인덱스로 계산하여 효율적인 접근이 가능합니다.
- 트리의 크기에 따라 배열의 크기가 정해지므로 메모리 공간 활용이 중요합니다.
- 하지만 트리의 구조가 동적으로 변경되는 경우 배열의 크기를 조정해야 하는 단점이 있습니다.
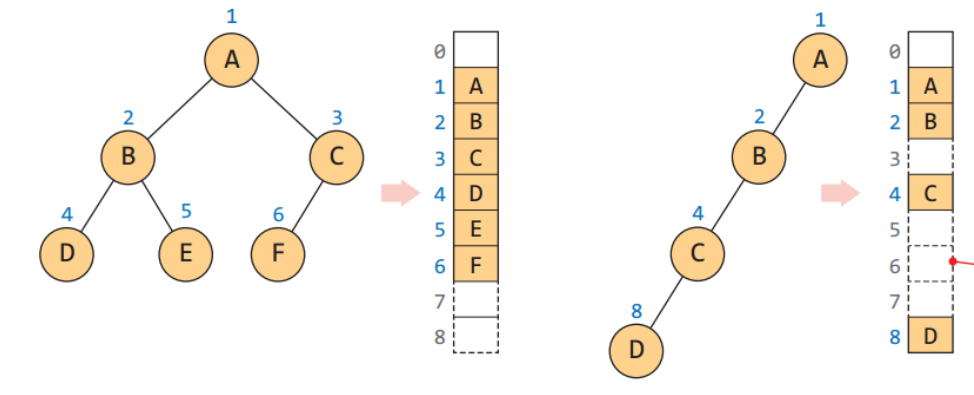
링크 표현법 (Link Representation):
- 이진 트리의 각 노드를 독립적인 객체로 표현하고, 객체들 간의 링크(포인터)를 통해 관계를 표현하는 방법입니다.
- 객체 지향 프로그래밍에서 자주 사용됩니다.
- 각 노드는 자신의 데이터와 왼쪽 자식 노드와 오른쪽 자식 노드를 가리키는 링크(포인터)를 가지고 있습니다.
- 트리의 구조를 동적으로 변경할 수 있으며, 메모리 공간을 효율적으로 활용할 수 있습니다.
- 하지만 포인터를 사용하기 때문에 추가적인 메모리 공간이 필요하고, 포인터 연산에 대한 오버헤드가 발생할 수 있습니다.

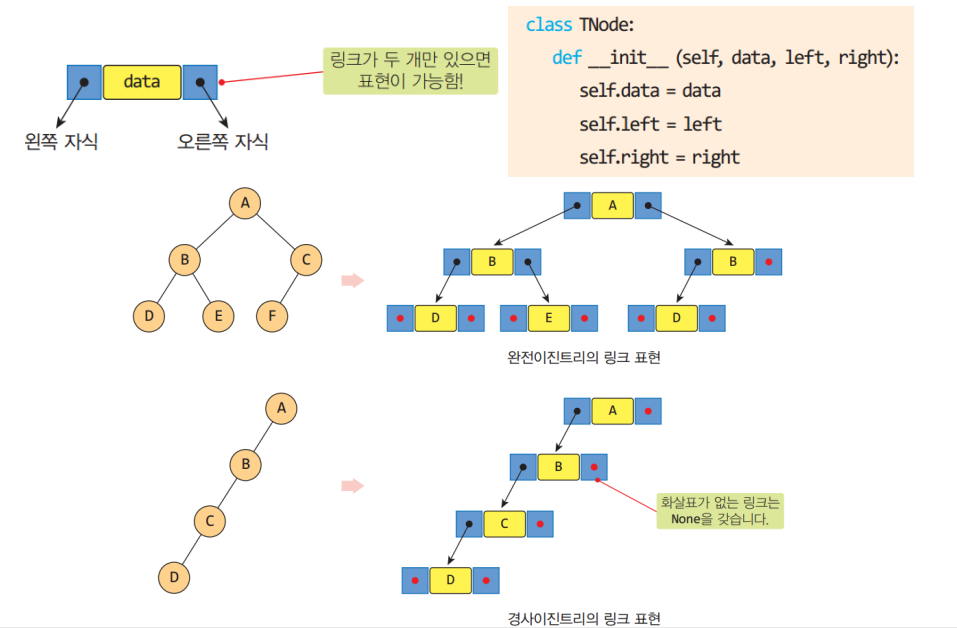
이진 트리의 표현 방법은 특정한 상황이나 문제에 따라 선택되어야 합니다. 배열 표현법은 트리의 구조가 정적이고 완전 이진 트리인 경우에 유용하며, 링크 표현법은 동적인 구조를 필요로 하는 경우나 트리의 크기가 변하는 경우에 유용합니다. 선택할 표현 방법은 메모리 사용, 접근 시간, 구현의 용이성 등을 고려하여 결정해야 합니다.

8.3 이진트리의 연산

순회(traversal):

트리에 속하는 모든 노드를 한 번씩 방문하는 것
트리에서 가장 기본적인 연산
선형 자료구조는 순회가 단순
트리는 다양한 방법이 있음

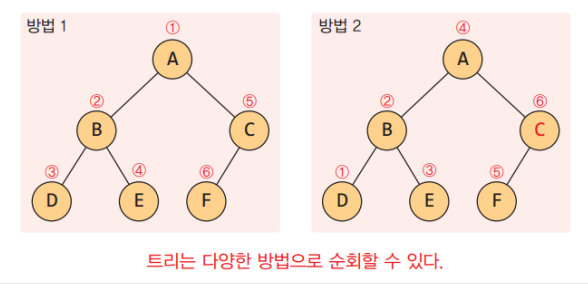
이진 트리의 순회 방법은 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal) 세 가지가 있습니다. 각각의 순회 방법은 트리의 노드를 어떤 순서로 방문하는지를 나타냅니다.

전위 순회 (Preorder Traversal):
- 노드를 다음 순서로 방문합니다: 루트 노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리
- 주로 노드의 값을 출력하는 용도로 사용됩니다.
- 루트를 가장 먼저 방문하고, 그 다음에 왼쪽 서브트리를 순회한 후 오른쪽 서브트리를 순회합니다.
중위 순회 (Inorder Traversal):
- 노드를 다음 순서로 방문합니다: 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브트리
- 이진 탐색 트리에서 정렬된 값을 출력하기 위해 주로 사용됩니다.
- 왼쪽 서브트리를 순회한 후 루트를 방문하고, 마지막으로 오른쪽 서브트리를 순회합니다.
후위 순회 (Postorder Traversal):
- 노드를 다음 순서로 방문합니다: 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 노드
- 주로 트리의 구조를 해체하거나 메모리를 해제하는 용도로 사용됩니다.
- 왼쪽 서브트리와 오른쪽 서브트리를 순회한 후에 마지막으로 루트를 방문합니다.